Building a generic heap in c++

Introduction

Heaps are a common and useful data structure in the software engineering world. In addition to serving as a basis for a priority queue, the heap is also the fundamental data structure used in heap sort. A heap is a complete binary tree that satisifies the heap property. The heap property is defined in reference to the heap type:

• A min heap follows the min heap property:

• A max heap follows the max heap property:

In this post, we’ll explore heaps. We’ll give some examples of both min- and max-heaps, we’ll present an analysis of the computational complexity, and we’ll write a generic heap implementation in C++. Let’s get started!

Min-heaps and Max-heaps

As we saw above, there are two types of heaps: min heaps and max heaps. Informally, a min heap is heap in which for all nodes, the parent node is larger than its children. Here’s an example of a max heap:

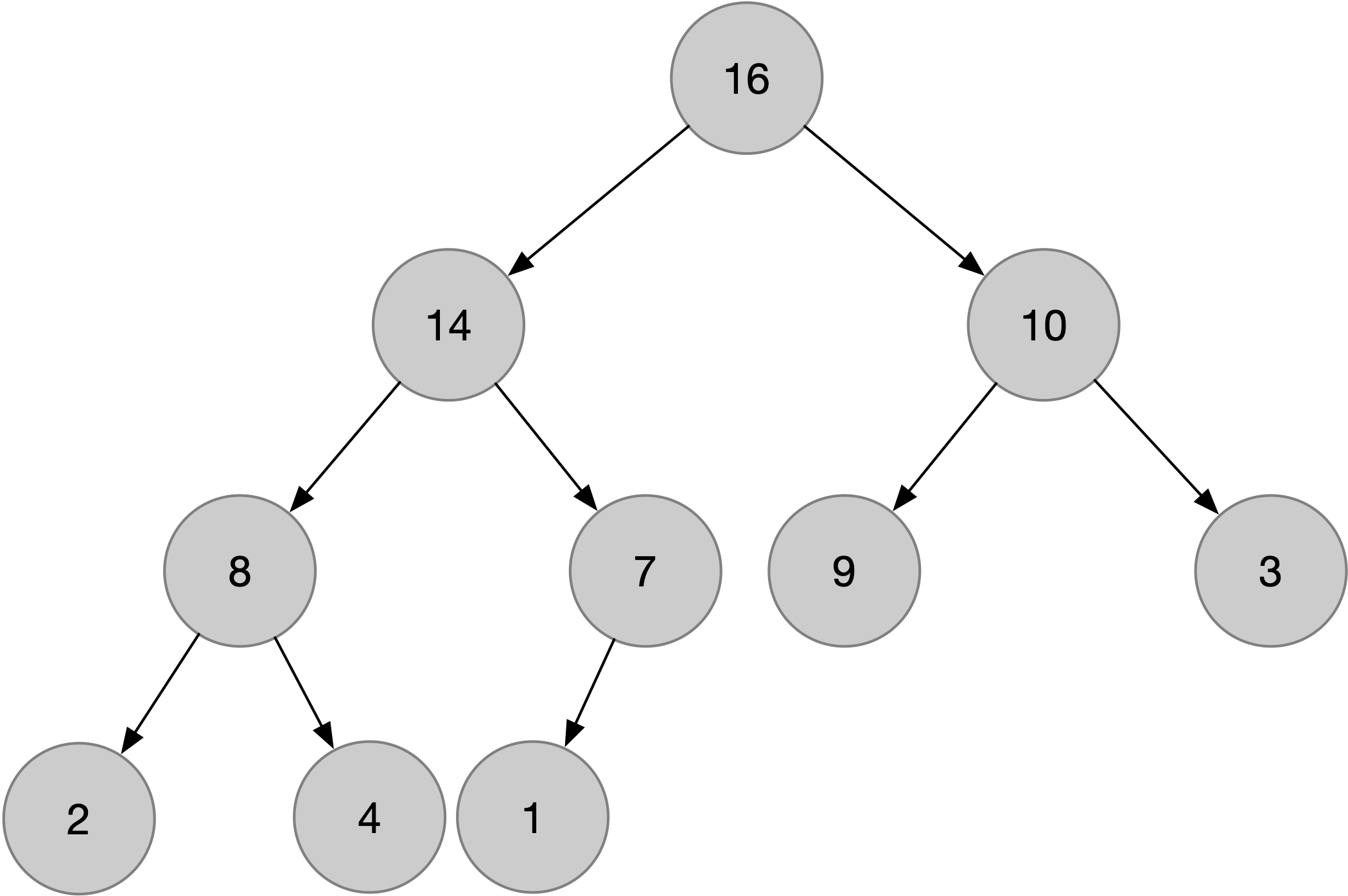
A max heap can be represented as an array, as shown below:

These are the same elements, organized as a min heap:

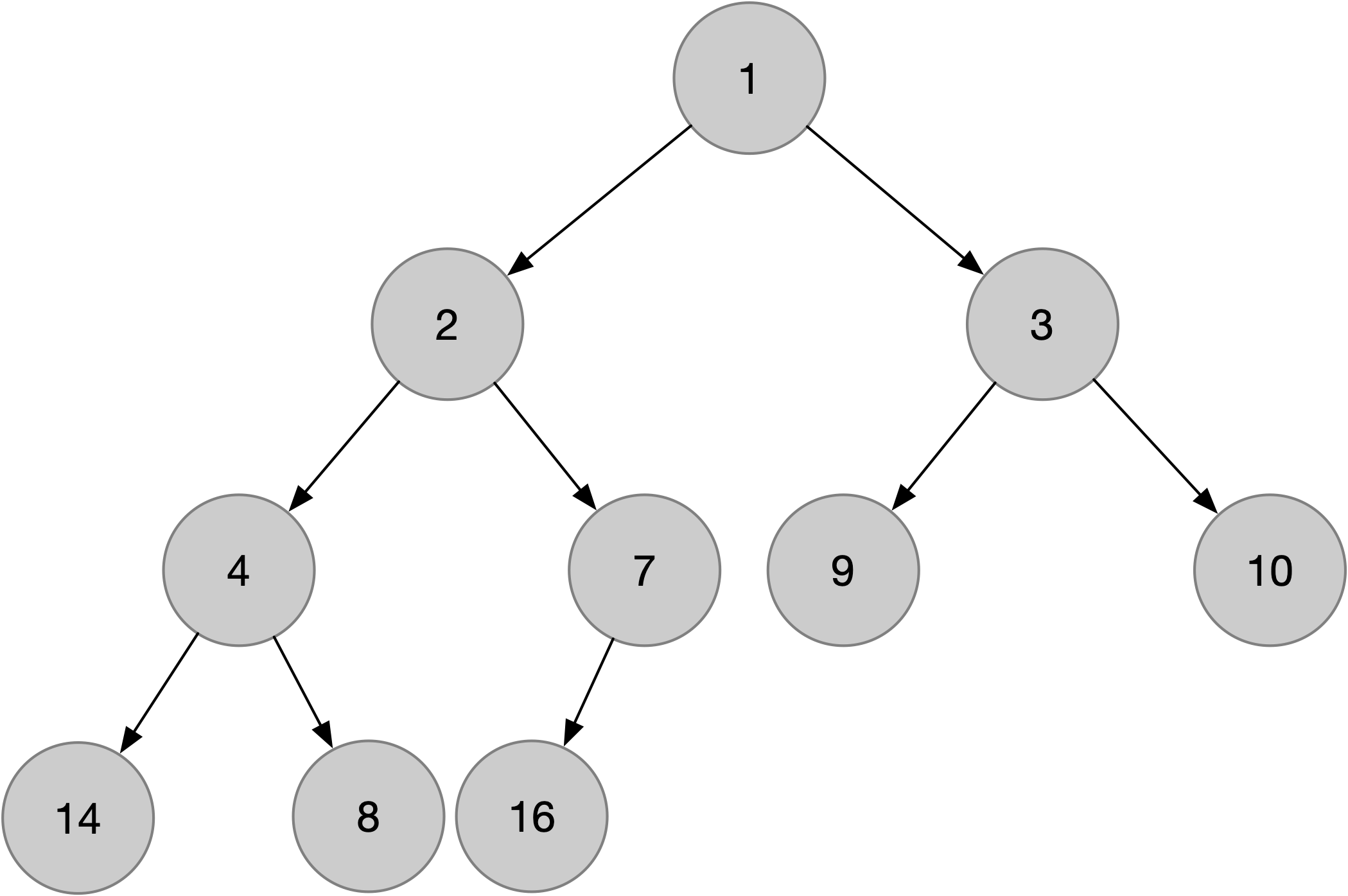
In array form:

In (Cormen et al., 2009), the array is 1-indexed, but that’s atypical for most programming languages. Hence, their formula for computing the index of the children given the index of a parent must be slightly modified, resulting in:

Generic Implementation in c++

For our simple heap implementation, we’ve chosen to implement only four basic methods:

• build - a method that builds a heap from an array (explained below).
• heapify - a method to perform the heapify operation (explained below).
• left & right (as defined above).

Note that this class is generic in two ways:

1. It uses a template parameters (c++ generics) to allow a heap to be of any type.
2. The caller must specify a predicate used to compare elements in the heapify method. This faciliates (1), but also allows for the use of a lambda to specify the heap type.

1
2
3
4
5
6
7
8
9
10
11
12
template<class T>
class GenericHeap : Heap<T> {
public:
    GenericHeap(std::function<bool(T,T)> predicate);
    void build(T *A, int length) override;
private:
    std::function<bool(T,T)> predicate;

    void heapify(T *A, int index, int length) override;
    int left(int index);
    int right(int index);
};

Since the build method relies on heapify, let’s look at the implementation of heapify first:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
template <class T>
void GenericHeap<T>::heapify(T *A, int index, int length) {
    int l = left(index);
    int r = right(index);
    int extremumIndex = index;

    if(l < length && predicate(A[l], A[extremumIndex])){
        extremumIndex = l;
    }

    if(r < length && predicate(A[r], A[extremumIndex])){
        extremumIndex = r;
    }

    if(extremumIndex != index){
        T temp = A[index];
        A[index] = A[extremumIndex];
        A[extremumIndex] = temp;

        heapify(A, extremumIndex, length);
    }
}

The variables l & r hold the indices of the left- and right-child of the current node. extrumumIndex (admittedly, an akward name) holds the index of the largest or smallest index (depending on the predicate). Suppose the predicate is the appropriate predicate for a integer based max heap:

1
std::function<bool(int, int)> maxHeapLambda = [](int a, int b) { return a > b; };

The conditional statements start on line 7 & 11 will find the index of the largest node of the {parent, left child, right child}. Then, the conditional statement starting at line 15 will swap the largest with the parent (if necessary). To create a min heap, we only have to reverse the comparison operator. A full instantiation looks like this:

1
2
3
4
5
6
int array[] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
int heapSize = 10;

std::function<bool(int, int)> maxHeapPredicate = [](int a, int b) { return a > b; };
auto maxHeap = new GenericHeap<int>(maxHeapLambda);
maxHeap->build(array, heapSize);

Where build() is defined as:

1
2
3
4
5
void GenericHeap<T>::build(T *A, int length) {
    for(int i = (int)(floor((length) / 2)); i >=0; i--){
        heapify(A, i, length);
    }
}

Runtime analysis

As stated above, a heap is a complete binary tree (a binary tree with all levels completely filled, except the last). This means that the height of the tree is $\Theta(\lg{n})$. Considering build() makes n calls to heapify(), a loose computational bound on the build() procedure is $O(n\lg{n})$. See (Cormen et al., 2009) for a asymptotically tight bound (hint: heapify runtime varies with the height of the node in the tree).

References

1. Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms, 3rd Edition. MIT Press.